Exploring Land Cover Data (Impact Observatory)

Exploring Land Cover Data (Impact Observatory)#

General Exploration Standard Python

Context#

Purpose#

Introduce manipulation and exploratory analysis of classified land use and cover data, using example data created by Impact Observatory from ESA Sentinel-2 imagery.

Dataset description#

There are now many classified (categorical) land cover data products freely available that are useful for Environmental Data Science. These include:

ESA CCI land cover, 300m spatial resolution global extent for years 1992-2015
Copernicus Global Land Cover, 100m spatial resolution global extent for years 2015-2019
USGS LCMAP, 30m spatial resolution for USA for years 1985-2020
UKCEH LCMs, various spatial resolutions for UK for various years 1990-2020
mapbiomas, 30m spatial resolution for Brazil for years 1985-2020
Impact Observatory, 10m spatial resolution global extent for 2017-2021

These products are provided as 2D rasters (spatial) or 3D data cubes (spatio-temporal). The number and classification of discrete land cover classes varies between products, but at their most basic will distinguish between broad land covers such as ‘crops’, ‘forest’ and ‘built-up’. The nominal (categorical) character of the data influences the types of analysis appropriate.

This notebook uses data created by Impact Observatory. The data are a time series for 2017-2021 of annual global land use and land cover (LULC) mapped at 10m spatial resolution. The data are derived from ESA Sentinel-2 imagery with each annual map specifying individual pixels as belonging to one of 9 LULC classes. The Impact Observatory LULC model uses deep learning methods to infer a single annual LULC class for each pixel in a Sentinel-2 image. Each annual global LULC map is produced by aggregating multiple inferences for images from across a given year (requiring processing approximately 2 million images to create each annual map).

Highlights#

Fetch land cover product data from an online repository
Visualise the data (maps and spatio-temporal plots)
Analyse aggregate change through bar charts and similar visualisation
Analyse pixel-by-pixel change including use of sankey diagrams
Analyse zonal change using ancillary vector data

Contributions#

Notebook#

James Millington (author), Dept of Geography, King’s College London, @jamesdamillington
Anne Fouilloux (reviewer), Dept of Geosciences, University of Oslo, @annefou
Amandine Debus (reviewer), Dept of Geography, University of Cambridge, @aedebus

Dataset originator/creator#

Esri (licensor)
Impact Observatory (processor, producer, licensor)
Microsoft (host)

The data are available under a Creative Commons BY-4.0 license.

Dataset reference and documentation#

Krishna Karra, Caitlin Kontgis, Zoe Statman-Weil, Joseph C. Mazzariello, Mark Mathis, and Steven P. Brumby. Global land use / land cover with sentinel 2 and deep learning. In 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, volume, 4704–4707. 2021. doi:10.1109/IGARSS47720.2021.9553499.
Impact Observatory. Methodology & accuracy summary. URL: https://www.impactobservatory.com/static/lulc_methodology_accuracy-ee742a0a389a85a0d4e7295941504ac2.pdf (visited on 2022-07-01).

Code#

Data loading code built on snippet from @acocac via ODC.stac docs and a Microsoft Planetary example notebook.

Load libraries#

Set project structure#

The next cell creates a separate folder to save any notebook outputs you should wish (e.g. below we use this directory in the demo of how you might load data from a local file).

notebook_folder = './notebook'
if not os.path.exists(notebook_folder):
    os.makedirs(notebook_folder)

1. Fetch and Load Data#

This notebook uses annual land cover data from Impact Observatory, 10m spatial resolution and global extent for 2017-2021. These data are hosted online by Microsoft’s Planetary Computer which enable you, the user, to run the code in the cloud (e.g. via binder).

Below we will use the pystac-client package to access STAC information from the Planetary Computer API, then read it using the odc-stac package. In doing so we will:

fetch data for a study area in Mato Grosso, Brazil
resample the original 10m spatial resolution to 300m (to decrease execution times in this example notebook)

Note

Fetching the data from the cloud adds some steps that would not be necessary had you already downloaded the data to your local machine. Consequently, in future for your own work you might ignore the Cloud Data code blocks and start from Local Data.

Cloud Data#

First we need to specify the location and extent of study area to fetch the relevant data. We do this by specying a bounding box around the center point of the study area.

#specify center point of the study area
x, y = (-56.1, -12.2)  #area in MT

#define a square bounding box for the study area
km2deg = 1.0 / 111 #1 deg corresponds to approximately 111 km at the equator
xd = 200 * km2deg
yd = 325 * km2deg
study_bbox_coords = [[x - xd, y - yd], [x - xd, y + yd], [x + xd, y + yd], [x + xd, y - yd]]

#view bounding box
study_bbox_coords

[[-57.9018018018018, -15.127927927927928],
 [-57.9018018018018, -9.27207207207207],
 [-54.2981981981982, -9.27207207207207],
 [-54.2981981981982, -15.127927927927928]]

We can then visualise the location and extent of the study area using hvPlot.

#create a GeoPandas GeoDataFrame 
study_poly = Polygon(study_bbox_coords)

crs = {'init': 'epsg:4326'}
sa_gpd = gpd.GeoDataFrame(index=[0], crs=crs, geometry=[study_poly])  

#interactive plot using hvplot.pandas
sa_gpd_interactive = sa_gpd.hvplot(
    geo=True,crs=sa_gpd.crs.to_epsg(),alpha=0.5, xlim=(-75, -35), ylim=(-30, 10),  tiles='CartoLight')
sa_gpd_interactive

With our study area defined, we can now query Microsoft Planetary Computer data that is available for this location using pystac-client.

catalog = pystac_client.Client.open("https://planetarycomputer.microsoft.com/api/stac/v1")

#https://pystac-client.readthedocs.io/en/latest/tutorials/pystac-client-introduction.html#API-Search
query = catalog.search(
    collections=["io-lulc-9-class"],
    limit=100,
    bbox=study_poly.bounds
)

#https://pystac-client.readthedocs.io/en/latest/tutorials/pystac-client-introduction.html#Items
items = list(query.get_items())
print(f"Found: {len(items):d} datasets")

print(items)

Found: 6 datasets
[<Item id=21L-2022>, <Item id=21L-2021>, <Item id=21L-2020>, <Item id=21L-2019>, <Item id=21L-2018>, <Item id=21L-2017>]

For the available datasets we can access and view the associated metadata.

stac_json = query.get_all_items_as_dict()     # Convert STAC items into a GeoJSON FeatureCollection
gdf = gpd.GeoDataFrame.from_features(stac_json)  #convert GeoJSON to GeoPandas to view nicely
gdf.head()

	geometry	datetime	proj:bbox	proj:epsg	io:tile_id	proj:shape	end_datetime	proj:transform	start_datetime	io:supercell_id
0	POLYGON ((-54.00000 -8.00195, -54.00000 -16.00...	None	[169256.89710350562, 8228747.785209756, 830736...	32721	21L	[88695, 66148]	2023-01-01T00:00:00Z	[10.0, 0.0, 169256.89710350562, 0.0, -10.0, 91...	2022-01-01T00:00:00Z	21L
1	POLYGON ((-54.00000 -8.00195, -54.00000 -16.00...	None	[169256.89710350562, 8228747.785209756, 830736...	32721	21L	[88695, 66148]	2022-01-01T00:00:00Z	[10.0, 0.0, 169256.89710350562, 0.0, -10.0, 91...	2021-01-01T00:00:00Z	21L
2	POLYGON ((-54.00000 -8.00195, -54.00000 -16.00...	None	[169256.89710350562, 8228747.785209756, 830736...	32721	21L	[88695, 66148]	2021-01-01T00:00:00Z	[10.0, 0.0, 169256.89710350562, 0.0, -10.0, 91...	2020-01-01T00:00:00Z	21L
3	POLYGON ((-54.00000 -8.00195, -54.00000 -16.00...	None	[169256.89710350562, 8228747.785209756, 830736...	32721	21L	[88695, 66148]	2020-01-01T00:00:00Z	[10.0, 0.0, 169256.89710350562, 0.0, -10.0, 91...	2019-01-01T00:00:00Z	21L
4	POLYGON ((-54.00000 -8.00195, -54.00000 -16.00...	None	[169256.89710350562, 8228747.785209756, 830736...	32721	21L	[88695, 66148]	2019-01-01T00:00:00Z	[10.0, 0.0, 169256.89710350562, 0.0, -10.0, 91...	2018-01-01T00:00:00Z	21L

The global LULC datasets are for ‘tiles’ covering regions of the earth’s surface - each line in the DataFrame above is for one year for tile 21L. We can also plot to show the study area does not cover multiple land cover tiles.

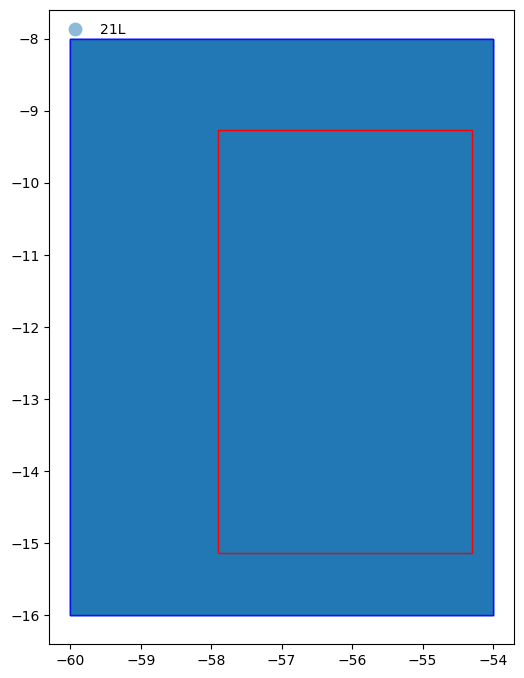
../../../_images/bccf480b5532d05dd045f4ad07b3c6bb892f05678bcd643c66caaebf32744673.png

From the figure above we can see the whole study area (represented by the red rectangle) is within in the tiles (represented by the blue rectangles) returned by the pystac query.

Now we are happy we know what datasets we wish to fetch, we can use odc-stac to fetch and load the data into memory, specifying the projection and spatial resolution we want as well as how we want data grouped in layers:

The data object we have created is an xarray Dataset which is a dict-like collection of DataArray objects with aligned dimensions. We can check the dimensions, coordinates, data and attributes (see xarray terminology):

lcxr

<xarray.Dataset> Size: 143MB
Dimensions:      (y: 2225, x: 1338, time: 6)
Coordinates:
  * y            (y) float64 18kB -1.037e+06 -1.037e+06 ... -1.704e+06
  * x            (x) float64 11kB -6.446e+06 -6.445e+06 ... -6.045e+06
    spatial_ref  int32 4B 3857
  * time         (time) datetime64[ns] 48B 2017-01-01 2018-01-01 ... 2022-01-01
Data variables:
    data         (time, y, x) int64 143MB dask.array<chunksize=(1, 2225, 1338), meta=np.ndarray>

Load Local Data#

In the previous section we fetched data from an online repository and loaded it into memory. In the sections below we will continue to work with that (and you can skip to the next section now, if you don’t want to see how to save and/or read data from a local drive).

The recommended way to store xarray data structures is netCDF, a binary file format for self-described datasets that originated in the geosciences.

For example, to save the xarray Dataset we created above on disk as netCDF, we would use something like:

lcxr.to_netcdf(os.path.join(notebook_folder,"MT-study-area.nc"))

Then to load the local netCDF file into a xarray Dataset we would use:

lcxr_disk = xr.open_dataset(os.path.join(notebook_folder,"MT-study-area.nc"), decode_coords="all")

Tip

If you have saved this notebook to a local machine, try uncommenting the code below and running it. Check you can see where the data has been saved on your local machine and note how the Dataset loaded is identical to the one you saved.

#lcxr.to_netcdf(os.path.join(notebook_folder,"MT-study-area.nc"))
#lcxr_disk = xr.open_dataset(os.path.join(notebook_folder,"MT-study-area.nc"), decode_coords="all")
#lcxr_disk

2. Visualisation#

Our dataset contains a 2D raster layer of land cover types for individual snapshots in time. Each map is a composite of land use/cover predictions for 9 classes throughout the year in order to generate a representative snapshot of each year.

We can visualise these spatio-temporal data in a variety of different ways, both static and interactive. But before exploring these, we will create a matplotlib colormap to display the 9 land cover classes with intuitive colors.

{'No Data': 0, 'Water': 1, 'Trees': 2, 'Flooded vegetation': 4, 'Crops': 5, 'Built area': 7, 'Bare ground': 8, 'Snow/ice': 9, 'Clouds': 10, 'Rangeland': 11}

from_list

under

bad

over

Note

Note that there are more than 9 colours in the colormap created - that’s because we also have colours for ‘No Data’ and for class IDs that are not used (skipped) in the data (e.g. there’s no land cover class 6 - we’ll label these as No Data below).

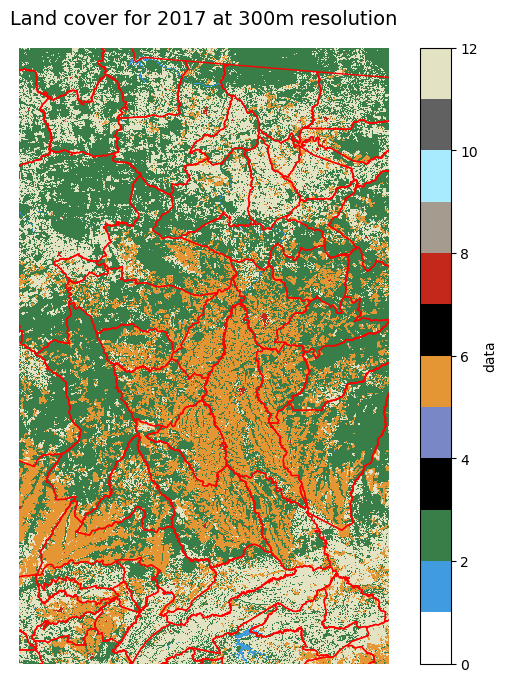
Now we can use the colormap with matplotlib to plot a static 2D map for a given time point.

../../../_images/40587dd1269648bb37f3943968d44e6f1ed99e2447a9d08a9b3c5994db0b9516.png

Similarly, we could make a static plot showing maps for each point in time to visually examine change.

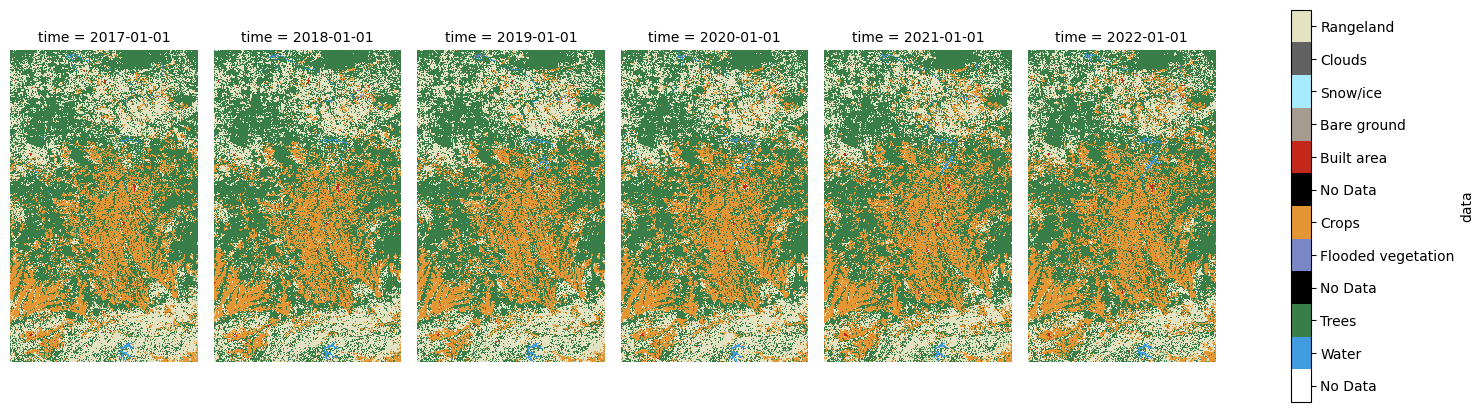
../../../_images/2043661719b47adca1c7c525f32ec6063fefcd970ce068e01902fe63a1dc1144.png

We can use holoviews to create an interactive plot - you should be able to use the slider below to see change through time in the same space.

3. Analysing Aggregate Change#

In this section we’re going to examine land cover change across the study area. Our aim is to produce a bar plot that shows increases or decreases in land area for each land cover class between two points in time.

We can quickly identify the unique values in our land cover maps and how many times they are observed (i.e. how many pixels fall in each land cover class). We can use numpy’s .unique function to count the occurrence of each value, then output as a Pandas DataFrame.

#list to hold pixel counts, class ID:name dict as list to append to 
counts_ls = [values_to_classes]

#loop over items
for i, j in enumerate(items):
    lcmap = lcxr.isel(time=i).to_array("band")            #get pixels for this year as an array
    unique, counts = np.unique(lcmap, return_counts=True)  #get the unique values and corresponding counts 
    lcmap_counts = dict(zip(unique, counts))               #combine them into a dict for easier viewing
    counts_ls.append(lcmap_counts)    

counts_df = pd.DataFrame(counts_ls).T     #create df from list and transpose

#create list of data years as string
counts_yr = list(lcxr["time"].values.astype('datetime64[Y]').astype('str'))  

counts_yr.insert(0, "Land Cover")        #insert 'LC'
counts_df.columns = counts_yr            #then use as df header
counts_df                                #print

	Land Cover	2017	2018	2019	2020	2021	2022
0	No Data	NaN	NaN	NaN	NaN	NaN	NaN
1	Water	11414	12011	13848	13921	14273	14892
2	Trees	1485124	1506206	1489276	1474662	1477771	1472174
4	Flooded vegetation	1157	1532	2369	1435	1358	1437
5	Crops	683380	678552	685153	737470	793002	833377
7	Built area	5583	5882	5929	6243	6546	6973
8	Bare ground	4859	2589	6022	6758	5217	4654
9	Snow/ice	NaN	NaN	NaN	NaN	NaN	NaN
10	Clouds	NaN	NaN	NaN	NaN	NaN	NaN
11	Rangeland	785533	770278	774453	736561	678883	643543

It might be more intuitve (and useful) to work in units of area (e.g. square km) rather than pixel counts, so let’s convert the pixel counts to area (sq km):

def cell_to_sqkm(x):
    return x * ((datares*datares) / 1000000)

sqkm_df = counts_df.copy(deep=False)
sqkm_df.loc[:,'2017':] = sqkm_df.loc[:,'2017':].apply(cell_to_sqkm)

sqkm_df

	Land Cover	2017	2018	2019	2020	2021	2022
0	No Data	NaN	NaN	NaN	NaN	NaN	NaN
1	Water	1027.26	1080.99	1246.32	1252.89	1284.57	1340.28
2	Trees	133661.16	135558.54	134034.84	132719.58	132999.39	132495.66
4	Flooded vegetation	104.13	137.88	213.21	129.15	122.22	129.33
5	Crops	61504.2	61069.68	61663.77	66372.3	71370.18	75003.93
7	Built area	502.47	529.38	533.61	561.87	589.14	627.57
8	Bare ground	437.31	233.01	541.98	608.22	469.53	418.86
9	Snow/ice	NaN	NaN	NaN	NaN	NaN	NaN
10	Clouds	NaN	NaN	NaN	NaN	NaN	NaN
11	Rangeland	70697.97	69325.02	69700.77	66290.49	61099.47	57918.87

We can see that some land cover classes are not present in any year (indicated by NaN). We’ll drop these and also reshape the data from ‘wide’ to ‘long’ for plotting.

sqkm_df = sqkm_df.dropna()    #drop No Data rows

#make data long
sqkm_df_long = pd.melt(sqkm_df, id_vars=['Land Cover'])
sqkm_df_long.rename(columns={'variable':'Year','value':'Area (sq km)'}, inplace = True)

From the Pandas DataFrame we can create both static and interactive bar plots. Here’s the static version with matplotlib.

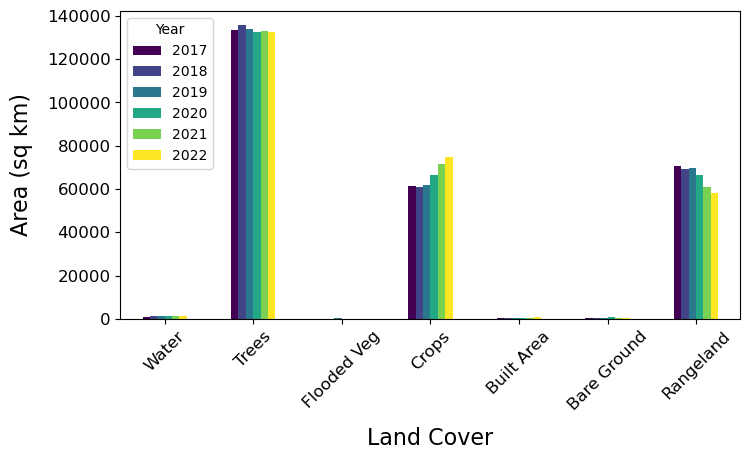
../../../_images/9ea6143063287b994f4463ed4a71270c4a2b2bdb61adfa211a85eb8fec990736.png

Tip

We could also do an interactive plot with hvplot for Pandas data (see the cell below).

Note

From the plots above we can see that through time the Trees and Rangeland classes have decreased in area, while Crops has increased.

We could also show this by calculating and plotting the change between first and final time snapshot.

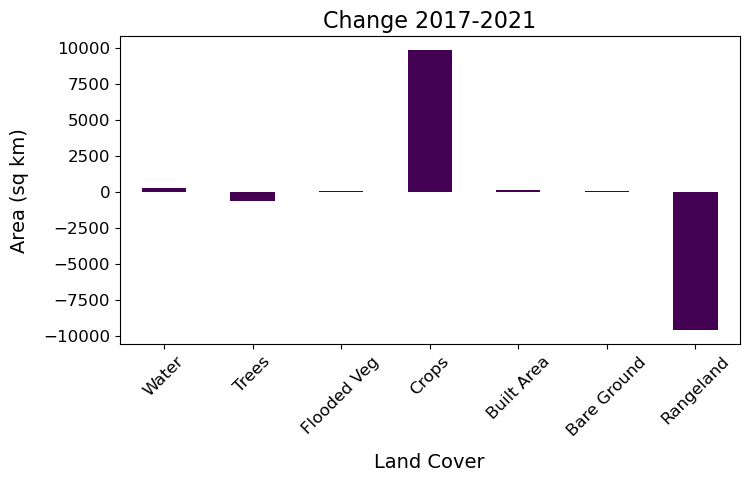
../../../_images/90e4bbf8c5b83eb1455f5ef4ed98ea9419fb6cb0e0b5241b93feeeb3e087b130.png

4. Analysing Pixel-by-Pixel Change#

In the last section we saw overall change in the land covers (e.g. decrease in Trees and Rangeland, increase in Crops). But which classes were changing to which other classes?

To understand the transitions between each class we need to analyse change for each pixel individually. We’ll enumerate individual pixels’ transitions for the first and last time snapshots using the a confusion matrix (using a function from sklearn and then visualise using a Sankey diagram (using holoviews).

First, the confusion matrix.

#connvert xarray DataArrays to numpy arrays
lc2017 = lcxr.sel(time='2017').isel(time=0).to_array("band").values.flatten()
lc2021 = lcxr.sel(time='2021').isel(time=0).to_array("band").values.flatten()

#create the confustion matrix using sklearn
conf = metrics.confusion_matrix(lc2017, lc2021)

#output as Pandas DF (drop no data land covers)
conf_pd = pd.DataFrame(conf,
                       index=sqkm_df[sqkm_df['2017'] != None]['Land Cover'],
                       columns=sqkm_df['Land Cover'])
conf_pd

Land Cover	Water	Trees	Flooded vegetation	Crops	Built area	Bare ground	Rangeland
Land Cover
Water	10185	473	66	74	10	5	601
Trees	2577	1410068	245	23500	180	504	48050
Flooded vegetation	214	100	678	7	0	15	143
Crops	167	9397	3	638037	476	1746	33554
Built area	5	60	1	125	5227	5	160
Bare ground	15	179	42	2221	15	1251	1136
Rangeland	1110	57494	323	129038	638	1691	595239

From the docs, the result is a:

confusion matrix whose i-th row and j-th column entry indicates the number of samples with true label being i-th class and predicted label being j-th class.

So for us, this means 2017 classes are the rows, with 2021 classes in columns (there are no predictions here - the 2021 observations are in place of any prediction). The number of cells that did not change are on the diagonal.

Note

This shows the most frequent transition was from Rangeland to Crops with 129,038 cells. Given that each cell is 9 hectares (300m x 300m) that means more than 1.1 million hectares (11,000 sq km) changed from pasture to cropland over the four years!

Now we can use the confusion matrix (after some manipulation) to create an interactive Sankey diagram using holoviews to visualise the transitions between each of the classes.

Using the data objects we created to make the Sankey diagram, we can also view the most frequent transitions in a table:

edges = list(zip(sourcelc, targetlc, conf_list))                   #edges as counts
trans_df = pd.DataFrame(edges, columns =['From', 'To', 'Count'])   #convert edges list of tuples to pandas df

nodes_dict = dict(zip(list(nodes['index']),list(nodes['label'])))  #create dictionary for next replace calls
trans_df['From'].replace(to_replace=nodes_dict, inplace=True)      #replace ids with labels
trans_df['To'].replace(to_replace=nodes_dict, inplace=True)        #replace ids with labels

trans_df = trans_df[trans_df['To'] != trans_df['From']]            #remove rows of 'no transition'
trans_df['Area (sqkm)'] = trans_df['Count'].apply(cell_to_sqkm)    #add area column
trans_df.sort_values('Count', ascending=False).head()              #output head, sorted

	From	To	Count	Area (sqkm)
45	Rangeland	Crops	129038	11613.42
43	Rangeland	Trees	57494	5174.46
13	Trees	Rangeland	48050	4324.50
27	Crops	Rangeland	33554	3019.86
10	Trees	Crops	23500	2115.00

Note

Now we can see that although large numbers of cells changed from Rangeland to other land covers, there were also relatively large numbers of cells changing into Rangeland. Check you can see this in the Sankey diagram above.

5. Analysing Zonal Change#

Above we have analysed the data for our entire study area and on a pixel-by-pixel basis. But sometimes we want to work at a level between the entire study area and individuals, using zones that belong to some kind of vector geography. This is where raster zonal statistics come in:

Zonal Statistics uses groupings to calculate statistics for specified zones.

The statistics are summary statistics (e.g. mean, median, standard deviation) of all the pixels that fall in each zone. The zones might be watersheds, biomes or ecoregions (physically) or states, countries, counties or census districts (socio-economically).

Here, we’ll use municipality boundaries as zones. For Brazil these are freely available online in (zipped) shapefile format which we can read using GeoPandas (which inherits from Pandas).

#load shapefile for municipalities
zipfile = "https://geoftp.ibge.gov.br/organizacao_do_territorio/malhas_territoriais/malhas_municipais/municipio_2021/UFs/MT/MT_Municipios_2021.zip"
munis = gpd.read_file(zipfile)
munis.head()

	CD_MUN	NM_MUN	SIGLA	AREA_KM2	geometry
0	5100102	Acorizal	MT	850.763	POLYGON ((-56.22987 -14.98368, -56.22538 -14.9...
1	5100201	Água Boa	MT	7549.308	POLYGON ((-53.09875 -13.63518, -52.93808 -13.6...
2	5100250	Alta Floresta	MT	8955.410	POLYGON ((-55.86740 -9.44394, -55.86829 -9.445...
3	5100300	Alto Araguaia	MT	5402.308	POLYGON ((-53.23920 -16.80826, -53.23884 -16.8...
4	5100359	Alto Boa Vista	MT	2248.414	POLYGON ((-51.40209 -11.57606, -51.40099 -11.5...

Data Manipulation#

Before we can use these data with the raster data we need to do some manipulation, including:

setting the dtype of the CD_MUN series appropriately
setting the map projection to be consistent with that for the raster land cover data (we’ll also do this for the study area polygon we made above)

#munis.dtypes                                  #check dtypes
munis['CD_MUN'] = munis['CD_MUN'].astype(int)  #set appropriate for muni code
#munis.crs                                     #check projection
munis = munis.to_crs(SMepsg)                   #reproject to match our raster data
sa_gpd = sa_gpd.to_crs(SMepsg)         #also reproject sa_polygon

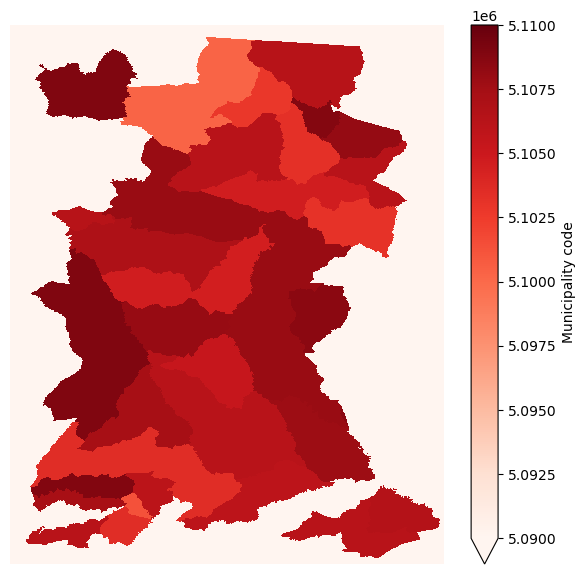
And now we can plot to check things are aligning nicely and to visualise our zones (municipalities).

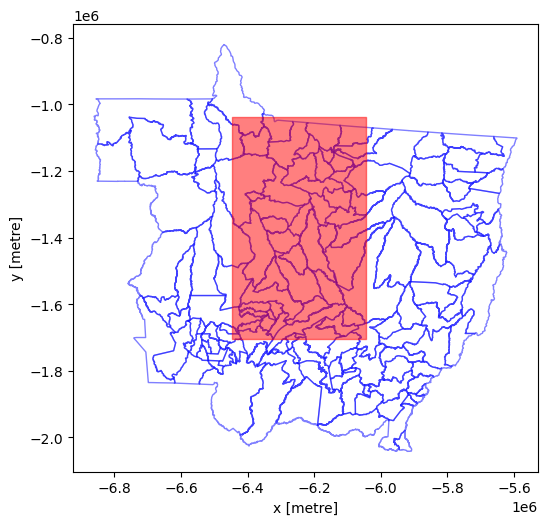
../../../_images/4b2f342de30e6fab7eb9e9b441dd42c0f7417062ba14380f776284f25556495b.png

Tip

We could also do an interactive plot with hvplot for Pandas data (not shown here to reduce notebook filesize - uncomment to run yourself).

#import hvplot.pandas  
#munis.hvplot(
#    geo=True,crs=munis.crs.to_epsg(),alpha=0.25, tiles=True) * sa_gpd.hvplot(
#    geo=True,crs=sa_gpd.crs.to_epsg(), alpha=0.25)

Let’s also make a static plot with matplotlib to visualise municipality boundaries over the raster land cover data.

../../../_images/763a0149f967ba9dfe9c072d24e64f8f33e09098d73b9d4f540378bc4f5b294c.png

Before we do our zonal statistics, to make comparison fair we will consider only those municipalities whose boundaries are completely within the study area.

First, remove municipalities from the vector shapefile that are not completely within the study area.

<Axes: >

../../../_images/4f93061084dafa8fa6bc2aa16dee99b1c88b6ae96f3a8a580338d75b7936a821.png

Next, create a raster from the new vector shapefile to mask cells from our land cover raster.

#collapse to list for rio.features.rasterize below
sa_munis_shapes = sa_munis[['geometry', 'CD_MUN']].values.tolist()

#get the spatial transform data needed for rio.features.rasterize below
lcxr_transform = lcxr['data'][0].rio.transform()   #this only works if rioxarray has been loaded - why? 

#create the mask raster (cells are CD_MUN for municipality polygons within study area, else -999)
sa_munis_r = rio.features.rasterize(sa_munis_shapes, fill=-999, 
                                    out_shape=lcxr['data'][0].shape, 
                                    transform=lcxr_transform) 

#create xarray DataArray from the new raster
sa_munis_xr = xr.DataArray(data=sa_munis_r,
                           name='Municipality code',
                           dims=["y", "x"],
                           coords={'y':('y',lcxr.y.data),
                                   'x':('x',lcxr.x.data)})

Let’s visualise the raster we’ve created from the vector shapefile of municipality boundaries.

../../../_images/e2736c899582ca7bd01a526a906b9dfc594c93b63f97377b18e72a614607f232.png

And finally, mask the existing land cover xarray DataSet with this new xarray DataArray.

#mask original land cover xarray with new xarray
lcxr_mask = lcxr.where(sa_munis_xr >0)  #nodata was set to -999

Now let’s check the mask worked by plotting the new (masked) land cover data with the municipality polygons overlaid.

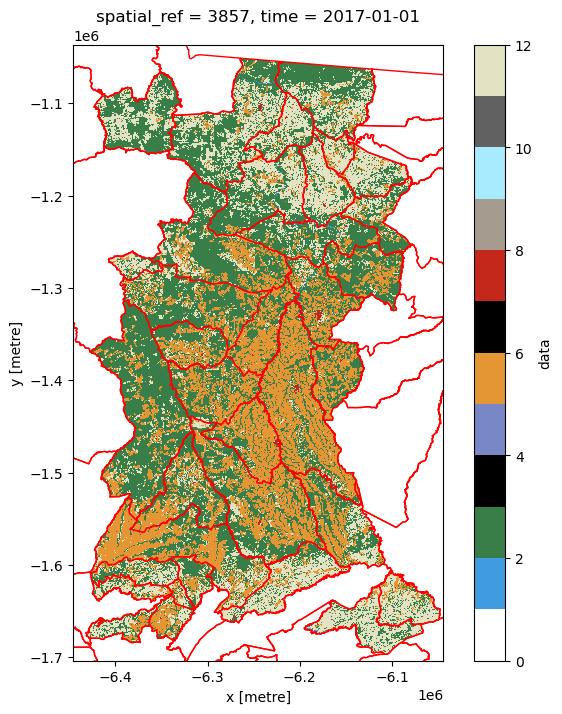
../../../_images/ba8974a27ec41d5d2d6254711adba23252efbf0c472b5217b4bd148ad770b4e8.png

Note

From this plot you should be able to start thinking about the land cover composition of each municipality, and how they might differ. For example, which are the municipalities with relatively high (or low) crop cover compared to rangeland cover?

One last piece of data manipulation is needed as the zonal_stats function we will use from the rasterstats package expects a 2D array in a format that can be read by the rasterio package (e.g. a numpy array). Hence data are for a single year of our data set.

lcxr_transform = lcxr_mask['data'][0].rio.transform()     #get the spatial transform info 
lcxr_17 = np.array(lcxr_mask['data'][0].astype('int32'))  #convert data for 2017 to numpy array

Zonal Stats#

Now we’re ready to actually calculate the statistics from the land cover raster by municipality shapefile polygon. When specifying that our input raster is categorical (as is the case for our land cover data), the zonal_stats function returns a list of dictionaries, one for each municipality polgyon. In turn, each dictionary provides cell counts (values) for each (land cover) class (keys).

#from rasterstats import zonal_stats
lcxr_17z = zonal_stats(sa_munis, lcxr_17,
                           affine=lcxr_transform,
                           categorical=True)
lcxr_17z   

[{1: 467, 2: 55424, 4: 1, 5: 6225, 7: 296, 8: 79, 11: 40802},
 {2: 1298, 5: 1340, 7: 71, 11: 2264},
 {1: 390, 2: 9892, 5: 1536, 7: 49, 8: 54, 11: 16024},
 {1: 76, 2: 28919, 5: 12480, 7: 79, 8: 90, 11: 3094},
 {1: 262, 2: 10150, 4: 12, 5: 2246, 7: 118, 8: 32, 11: 23202},
 {1: 4, 2: 3926, 5: 7005, 7: 28, 8: 3, 11: 4240},
 {1: 15, 2: 33223, 4: 7, 5: 49192, 7: 188, 8: 63, 11: 15496},
 {1: 34, 2: 14085, 4: 20, 5: 24556, 7: 39, 8: 284, 11: 972},
 {1: 20, 2: 17018, 4: 5, 5: 13094, 7: 80, 8: 147, 11: 3680},
 {1: 820, 2: 34203, 4: 79, 5: 6941, 7: 35, 8: 63, 11: 10356},
 {1: 90, 2: 12272, 5: 28703, 7: 340, 8: 107, 11: 1758},
 {1: 17, 2: 11858, 4: 21, 5: 5391, 7: 105, 8: 23, 11: 29141},
 {1: 26, 2: 8113, 5: 3555, 7: 39, 8: 16, 11: 4179},
 {1: 6, 2: 15114, 4: 2, 5: 4206, 7: 30, 8: 76, 11: 8255},
 {1: 618, 2: 9902, 5: 1429, 7: 17, 11: 27368},
 {1: 650, 2: 35901, 4: 16, 5: 5528, 7: 49, 8: 88, 11: 26713},
 {1: 40, 2: 51898, 4: 16, 5: 50012, 7: 264, 8: 333, 11: 10289},
 {1: 19, 2: 5981, 5: 2891, 7: 60, 11: 6914},
 {1: 412, 2: 39336, 4: 126, 5: 4792, 7: 34, 8: 62, 11: 22007},
 {1: 45, 2: 3675, 5: 847, 7: 18, 8: 3, 11: 6109},
 {1: 6, 2: 5861, 5: 3779, 7: 29, 8: 24, 11: 19387},
 {1: 133, 2: 49603, 4: 5, 5: 20542, 7: 49, 8: 423, 11: 9087},
 {1: 1, 2: 3764, 4: 1, 5: 2178, 7: 15, 11: 7941},
 {1: 16, 2: 27081, 4: 1, 5: 19384, 7: 88, 8: 98, 11: 6865},
 {1: 32, 2: 24314, 5: 20581, 7: 22, 8: 59, 11: 11259},
 {1: 280, 2: 19897, 4: 13, 5: 21250, 7: 812, 8: 286, 11: 3981},
 {1: 356, 2: 32036, 4: 7, 5: 71821, 7: 455, 8: 263, 11: 4285},
 {1: 35, 2: 58226, 4: 11, 5: 23880, 7: 76, 8: 244, 11: 15598},
 {1: 42, 2: 25238, 5: 23900, 7: 123, 8: 269, 11: 3141},
 {1: 8, 2: 8036, 4: 7, 5: 2251, 7: 45, 8: 32, 11: 17373},
 {1: 21, 2: 15438, 5: 19175, 7: 68, 8: 205, 11: 951},
 {1: 65, 2: 3043, 4: 61, 5: 1852, 7: 26, 8: 60, 11: 7849},
 {1: 1, 2: 9736, 4: 3, 5: 3474, 7: 23, 8: 13, 11: 9437},
 {1: 88, 2: 101187, 5: 23348, 7: 50, 8: 382, 11: 10755},
 {1: 20, 2: 36506, 5: 673, 7: 40, 8: 4, 11: 22004}]

Tip

It’s easier to analyse this output if we store it as a Pandas DataFrame.

lcxr_17z_pd = pd.DataFrame(lcxr_17z)                        #convert list of dicts to DataFrame
lcxr_17z_pd.set_index(sa_munis['NM_MUN'],inplace=True)      #use municipality name as index
lcxr_17z_pd.rename(columns=values_to_classes,inplace=True)  #rename columns using dict created above
lcxr_17z_pd = lcxr_17z_pd.add_suffix('17')                  #remind ourselves these data are for a given year
lcxr_17z_pd.head()     

	Water17	Trees17	Flooded vegetation17	Crops17	Built area17	Bare ground17	Rangeland17
NM_MUN
Alta Floresta	467.0	55424	1.0	6225	296	79.0	40802
Arenápolis	NaN	1298	NaN	1340	71	NaN	2264
Carlinda	390.0	9892	NaN	1536	49	54.0	16024
Cláudia	76.0	28919	NaN	12480	79	90.0	3094
Colíder	262.0	10150	12.0	2246	118	32.0	23202

We could examine these total counts, but in many ways it is more useful to consider the proportion of a muncipality that is covered by each land cover.

lcxr_17z_pd['sum17']=lcxr_17z_pd.sum(axis=1)                  #add column for total cells in the muni

lcxr_17prop_pd = pd.DataFrame(index = lcxr_17z_pd.index)      #create a new DataFrame to hold the proportions

#calculate proportion for each land cover
for column in lcxr_17z_pd.loc[:,'Water17':'Rangeland17']:
    lcxr_17prop_pd['{}-prop'.format(column)] = lcxr_17z_pd[column] / lcxr_17z_pd['sum17']  
    
lcxr_17prop_pd.head()

	Water17-prop	Trees17-prop	Flooded vegetation17-prop	Crops17-prop	Built area17-prop	Bare ground17-prop	Rangeland17-prop
NM_MUN
Alta Floresta	0.004521	0.536566	0.000010	0.060265	0.002866	0.000765	0.395008
Arenápolis	NaN	0.261009	NaN	0.269455	0.014277	NaN	0.455258
Carlinda	0.013956	0.353981	NaN	0.054965	0.001753	0.001932	0.573412
Cláudia	0.001699	0.646408	NaN	0.278957	0.001766	0.002012	0.069158
Colíder	0.007273	0.281772	0.000333	0.062351	0.003276	0.000888	0.644106

We could create a-spatial plots (e.g. bar plots) directly from this DataFrame. To create spatial plots (maps) we need to attach the spatial information for each municipality to create a GeoPandas GeoDataFrame:

lcxr_17prop_gpd = pd.merge(sa_munis, lcxr_17prop_pd, how='left', left_on = 'NM_MUN', right_index=True)
lcxr_17prop_gpd.head()

	CD_MUN	NM_MUN	SIGLA	AREA_KM2	geometry	Water17-prop	Trees17-prop	Flooded vegetation17-prop	Crops17-prop	Built area17-prop	Bare ground17-prop	Rangeland17-prop
2	5100250	Alta Floresta	MT	8955.410	POLYGON ((-6219130.124 -1056088.035, -6219229....	0.004521	0.536566	0.000010	0.060265	0.002866	0.000765	0.395008
12	5101308	Arenápolis	MT	417.337	POLYGON ((-6330913.103 -1615920.187, -6330922....	NaN	0.261009	NaN	0.269455	0.014277	NaN	0.455258
26	5102793	Carlinda	MT	2421.788	POLYGON ((-6212162.920 -1088961.922, -6211814....	0.013956	0.353981	NaN	0.054965	0.001753	0.001932	0.573412
29	5103056	Cláudia	MT	3843.561	POLYGON ((-6153965.646 -1263744.447, -6153909....	0.001699	0.646408	NaN	0.278957	0.001766	0.002012	0.069158
31	5103205	Colíder	MT	3112.091	POLYGON ((-6175226.198 -1146318.365, -6175285....	0.007273	0.281772	0.000333	0.062351	0.003276	0.000888	0.644106

And now we can do a static plot to visualise the proportion of two land covers across the municipalities.

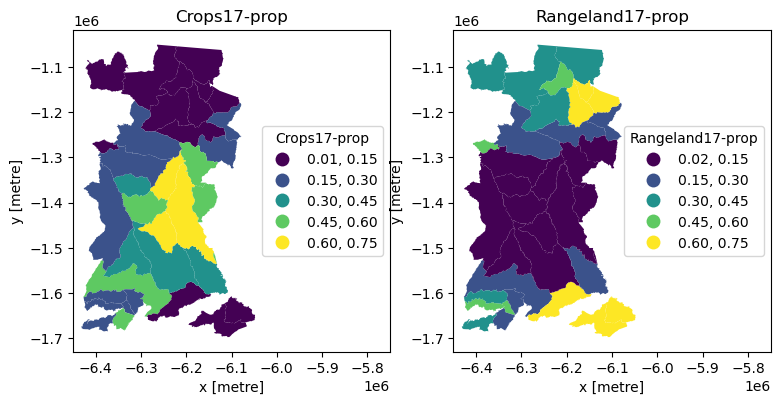
../../../_images/b4f834df8fc0c3d7e6dab3e964310d5be0a6ac2df92a10d658123cc57f1cdd15.png

An interactive plot enables linked pan/zoom of the two variables (although without consistent classification of polygons).

Note

From these plots we should be able to see what we might have expected from the raster data: municipalities in the north and south of the study area are dominated by rangeland, while those in the centre are dominated more by cropland. We might then think about what social, economic, political or other characteristics of the municipalities have led to this situation.

To examine change through time, we need to calculate the zonal stats for a second year, then calculate proportional change between the two time points. First the zonal stats.

	Water21	Trees21	Flooded vegetation21	Crops21	Built area21	Bare ground21	Rangeland21	sum21
NM_MUN
Alta Floresta	467	54865	1.0	9039	337	194.0	38391	103294.0
Arenápolis	2	1312	NaN	2032	76	NaN	1551	4973.0
Carlinda	390	9823	NaN	2617	49	80.0	14986	27945.0
Cláudia	607	26625	1.0	14700	65	76.0	2664	44738.0
Colíder	376	10263	3.0	4660	140	24.0	20556	36022.0

Now calculate the proportional change between the two years.

	Water-propD	Trees-propD	Flooded vegetation-propD	Crops-propD	Built area-propD	Bare ground-propD	Rangeland-propD
count	34.000000	35.000000	15.000000	35.000000	35.000000	31.000000	35.000000
mean	0.546392	0.013755	0.626822	0.414401	0.132359	0.264670	-0.218614
std	1.542047	0.092306	1.125911	0.465972	0.112021	1.151980	0.124551
min	-0.315789	-0.133255	-0.750000	0.001309	-0.177215	-0.666667	-0.518625
25%	-0.035096	-0.012748	0.000000	0.078856	0.074984	-0.253253	-0.319861
50%	0.013201	-0.006975	0.363636	0.231721	0.142857	-0.120419	-0.187844
75%	0.266516	0.011556	1.104396	0.607837	0.202041	0.273100	-0.125082
max	6.986842	0.430131	3.571429	2.257058	0.358974	5.500000	-0.014088

From the summary statistics we can already begin to see differences in the trajectories of change. To map change spatially we finally merge with the spatial information.

lcxr_1721prop_gpd = pd.merge(sa_munis, lcxr_1721prop_pd, how='left', left_on = 'NM_MUN', right_index=True)

Given that proportional change can be positive or negative, we should use a diverging colour palette.

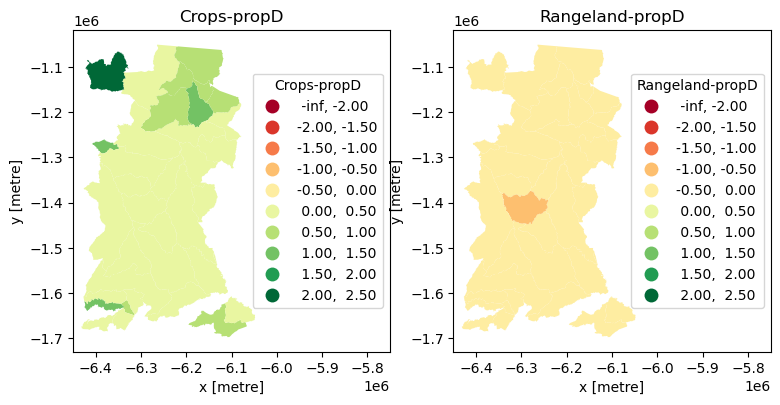
../../../_images/b54081e8243010a5ca7b9f6526762664da44bc7f33c7cd32bc104d86aad4ef29.png

This allows us to see that all municipalities decreased their Rangeland cover and increased their Cropland cover between 2017 and 2021, and to locate municipalities with extremes of change (which we could then go and further investigate).

Summary#

This notebook introduce manipulation and exploratory analysis of classified land cover data. Specifically, it:

used pystac-client to access information from the Microsoft’s Planetary Computer API and used that with odc-stac to read land cover raster data from an online repository.
used matplotlib and holoviews to visualise the spatio-temporal land cover data statically and interactively.
used from sklearn to create a matrix of pixel-by-pixel change and then holoviews to visualise that change using a Sankey diagram.
used rasterstats to analyse zonal change with tabular data and visualisations.

Citing this Notebook#

Please see CITATION.cff for the full citation information. The citation file can be exported to APA or BibTex formats (learn more here).

Additional information#

Dataset: 10m Annual Land Use Land Cover (9-class) from Impact Observatory for 2017-2021.

License: The code in this notebook is licensed under the MIT License. The Environmental Data Science book is licensed under the Creative Commons by Attribution 4.0 license. See further details here.

Contact: If you have any suggestion or report an issue with this notebook, feel free to create an issue or send a direct message to environmental.ds.book@gmail.com.

Notebook repository version: v1.0.6
Last tested: 2024-03-11

Exploring Land Cover Data (Impact Observatory)

Contents

Exploring Land Cover Data (Impact Observatory)#

Context#

Purpose#

Dataset description#

Highlights#

Contributions#

Notebook#

Dataset originator/creator#

Dataset reference and documentation#

Code#

Load libraries#

Set project structure#

1. Fetch and Load Data#

Cloud Data#

Load Local Data#

2. Visualisation#

3. Analysing Aggregate Change#

4. Analysing Pixel-by-Pixel Change#

5. Analysing Zonal Change#

Data Manipulation#

Zonal Stats#

Summary#

Citing this Notebook#

Additional information#